¿Cuál es la desviación estándar? ¿Cuáles son los tipos? ¿Cómo se calcula?

La desviación estándar es una medida del nivel de dispersión, es decir, indica lo uniforme que es un conjunto de datos. Es decir, cuanto mayor es la desviación estándar, el conjunto de datos es más uniforme. Desviación estándar, el conjunto de datos se aleja más de la media. Cuanto más cerca de 0 esté, tendremos una desviación estándar más homogénea. Compruebe en detalle qué es la desviación estándar en este artículo.
Compruebe también:
- Estadística descriptiva básica y centralidad
- Probabilidad: ¿qué es y cómo aplicar este concepto?
¿Qué es y cómo se hace una desviación estándar?
La desviación estándar es una medida de dispersión de un conjunto de datos, es decir, un coeficiente de variación de esos datos. Es habitual interesarse por la desviación típica de una población, por ejemplo. Sin embargo, utilizamos los datos de una muestra para estimar la desviación de una población a partir de la desviación de esa muestra.
Por ejemplo, en el caso de una biblioteca escolar: ¿cuántos libros han alquilado en el último mes? Así que tenemos a toda la población escolar involucrada, porque la pregunta se dirige a todos los estudiantes . En estos casos, se utiliza la varianza de la población.
Sin embargo, a veces no es posible encontrar información sobre toda una población y puede ser más fácil utilizar una muestra de 150 alumnos para estimar los datos de toda la población escolar. A partir de ahí, utilizamos estos resultados para determinar los hábitos de préstamo de la biblioteca para toda la población estudiantil. En estos casos, se utiliza la varianza de la muestra.
¿Cuál es la fórmula de la desviación estándar?
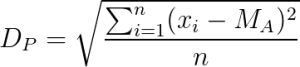
Figura I. Fórmula de cálculo de la desviación estándar
Dónde:
Dp: es la desviación;
Xi: es cualquier valor del conjunto de datos en la posición i;
MA: es la media aritmética del conjunto de datos;
n: es la cantidad total de datos en el conjunto de datos.
Ejemplo de desviación estándar
Ejemplo: En un equipo de baloncesto, los atletas tienen las siguientes alturas: 1,80, 1,95, 1,98, 1,88, 2,04. ¿Cuál es la altura media del equipo? ¿Y cuál es la desviación estándar de la altura del equipo?
Primero, al promediar, tenemos:

Media aritmética de los jugadores de baloncesto

Desviación estándar entre las alturas de los jugadores de baloncesto.
Varianza y desviación estándar
La varianza, al igual que la desviación, es también una medida de dispersión que indica la regularidad de un conjunto de datos en torno a la media. Es similar a la propia desviación estándar, ya que una se deriva de la otra. La varianza se calcula como el cuadrado de la desviación típica, lo que básicamente supone excluir la raíz cuadrada de la fórmula de la desviación típica, por lo que la varianza viene dada por:

Figura II. Fórmula para calcular la varianza
Desviación Estándar Excel (Paso a Paso)
Una herramienta muy utilizada en los cálculos estadísticos es Microsoft Excel, por lo que ahora enseñaremos a calcular la desviación estándar de una muestra utilizando dicho programa. Para ello, utilizaremos el ejemplo del equipo de baloncesto mencionado anteriormente.
Paso 1: Poner los datos en una sola columna.
Antes de iniciar el cálculo, hay que disponer los datos con los que se va a trabajar en la misma columna, como en la imagen siguiente.

2º Paso: Insertar la fórmula de la desviación estándar (DESVPAD.P)
Para insertar cualquier fórmula en Excel, primero hay que poner el signo de igualdad «=». Luego debe escribir la función DESVPAD.P y así, seleccionar el rango donde se encuentran los argumentos de la función, como en la imagen siguiente.

Paso 3: Por último, basta con pulsar la tecla «Intro» o «Retorno» y el resultado aparecerá en la celda donde se insertó la fórmula.
En la metodología six sigma se suele utilizar la desviación estándar para dar forma a las distribuciones de probabilidad. Como por ejemplo la distribución normal, muy característica de esta metodología y conocida como la distribución de probabilidad más importante. Vea a continuación una lección de vídeo sobre el análisis de datos del curso de estadística en Excel disponible en la Suscripción FM2S.
Además, con la Suscripción, también tienes acceso a los siguientes beneficios: grupos de networking para suscriptores, contenidos prácticos, mentoring online, profesores con amplia formación teórica y práctica, materiales y cursos exclusivos, webinars y otros eventos. No pierda tiempo y comience ya su transformación profesional.
¿Cuándo utilizar la desviación estándar de la muestra o de la población?
La mayoría de las veces, nos interesa conocer la desviación estándar de una población, es decir, una cantidad muy grande de datos. Eso es porque la población es nuestro objeto de interés. Por lo tanto, normalmente se calcularía la varianza de la población si:
- Tienes toda la población o;
- Tiene una muestra de una población mayor, pero sólo le interesa esta muestra y no quiere generalizar sus resultados a la población.
Sin embargo, en estadística, se utiliza generalmente con una muestra de la que se desea estimar (generalizar) una población, y la desviación estándar no es una excepción. Así que si todo lo que tienes es una muestra, pero quieres una declaración sobre la desviación de la población de la muestra, utilizas la desviación estándar de la muestra.
Por ejemplo, para calcular la altura media de los niños de un colegio de 1000 alumnos (población) no es necesario medir la altura de todos. Se toma una muestra de la población, es decir, 100 alumnos, y a partir de ella se estima la altura media.
Pero puede ocurrir un problema y hay que tener cuidado si se obtiene esta muestra con 100 estudiantes demasiado bajos, o demasiado altos que no sería una buena representación de su población. El truco consiste en estimar un tamaño de muestra que represente realmente a la población.
¿Cuáles son los tipos de variación?
La variación de causa común son los factores siempre presentes (es decir, los insumos o las condiciones del proceso) que contribuyen en diversos grados a cambios relativamente pequeños, es decir, que parecen ser aleatorios, en los resultados día tras día, semana tras semana.
Estos factores actúan de forma bastante independiente entre sí. El efecto colectivo de todas las causas comunes suele denominarse variación del sistema porque define la cantidad de variación inherente al sistema. Suele ser difícil, si no imposible, vincular la variación aleatoria de causa común a una fuente concreta.
Estos pueden incluir la variación compuesta inducida por el ruido, la vibración operativa y la eficiencia de la máquina, y generalmente son difíciles de identificar y evaluar porque son de naturaleza aleatoria. Sin embargo, si sólo existe una variación aleatoria, la salida del proceso forma una distribución estable en el tiempo.
Las variaciones por causas especiales son factores que inducen a la disparidad, además de la variación aleatoria. A menudo, la variación por causa especial aparece como un efecto extremo o algún patrón específico e identificable en los datos. Las causas especiales suelen denominarse causas asignables, ya que la variación producida se rastrea y atribuye a una fuente identificable.
Entre ellas se encuentra la variación inducida por efectos especiales no siempre presentes o incorporados al proceso. Ya que, algunos ejemplos incluyen: temperatura inducida y factores ambientales no controlados, sobrecargas, personas, cambios en el proceso, ajustes de la herramienta, error de medición y variaciones del material.
¿Quieres saber más?
¡Aprovecha para conocer los cursos gratuitos de FM2S!
Deixe seu comentário
FM2S


Deja una respuesta